相信很多人和我一样，刚开始学PBR的时候被一大堆名词直接搞懵逼：BRDF、GGX、半球积分、辐射度、立体角……都是些什么啊？这还没完，各种公式居然……全是积分！
所以我还是尽量简单的描述PBR中各个组成部分的意义，回避枯燥的推导过程直接看结果，让大家首先了解到整体的框架和思路。有兴趣的同学可以在本文之后继续研究其物理本质，没时间深究的同学也能照着公式读写代码。
回顾
首先我们回顾一下Blinn-Phong光照公式：
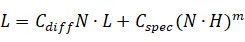
这是个常用的光照公式，其中：
是漫反射颜色；
是高光颜色，或者叫镜面反射的颜色；
是表面法线和光线方向的点乘，结果是两个向量的余弦，下文也写做
；
是表面法线和半角向量的点乘，也是它们的余弦，下文也写作
，半角向量是视线向量和光线向量的中间值，既Normalized(L + V), 顺便补充一下，下文还会把法线与视线的余弦写作
；m用来控制高光的扩散范围，越大时，光斑越集中，越小时，光斑约分散。
为了少写几个变量，同时让脑子少绕点弯，我们把公式改写成这样：
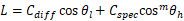
这个公式很简单，而且GPU计算起来也很高效，不过效果上确是一般般，下面介绍一版改进版本的公式：
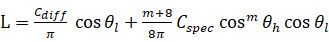
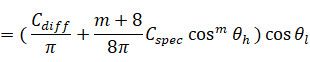
这个新公式的变化主要有三点：
1）Diffuse光增加了一个（1/π）的系数
，它会让我们在给光源设置Diffuse的时候更加直观，不过很多时候引擎会将这个步骤在内部预先进行处理。2）高光也增加了一个系数，这个系数很有意思：在原公式中，m越大高光的光斑越集中，加上这个参数后我们发现，m越大除了让光斑越集中，还能让高光更亮。这是很合理的物理现象，光的能量越密集，单位面积上的强度就越大，总能量不变。这个做法叫“归一化”。
3） 此外高光部分还增加了与
相乘的部分，有点类似Diffuse了。这个其实是更接近真实的情况，因为所有光线照射的效果都需要考虑受光面倾斜的情况，只是老公式认为在高光部分这个影响不明显，于是省略掉以节省性能开销。分析
当我们在渲染中使用这个公式时，效果已经漂亮不少了。现在我可以告诉大家什么是传说中的BRDF了：
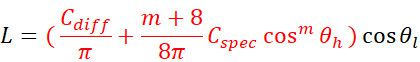
我们看括号里的部分，这就是一个BRDF。
BRDF不是一个公式，是一类公式，学名“双向反射分布函数”，说人话就是：给一个入射角度和一个观察角度，它能给出一个决定最终射向观察角度的光的强度的系数（这样的说法并不严谨，但在本文中按这样理解没太大毛病），凡是干这个事情的都叫BRDF函数，有的BRDF函数离真实物理法则更接近，有的则假得一逼。常用的Unity引擎中就包含了三套BRDF公式，用作不同性能机型的适配。
在上面的公式中，红字部分就是计算这样的一个系数，留意半角向量是入射向量和观察向量共同计算出来的。我们把BRDF单独抽出来写是这样的：
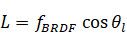
下面我们只看BRDF，给这个公式的每个成分再赋予一些意义，让它显得高大上一点。
第一部是一个Lambert光照公式，用来计算Diffuse，纳尼？好像还缺个
？注意注意，这个已经被抽取到括号外了，也就是BRDF公式之外，所以括号中的BRDF部分中，我们认为Lambert光照就是第一部分。
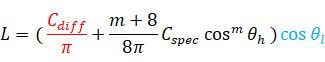
现在我们再看一下高光部分：
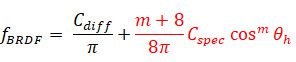
首先我们看
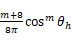这个部分，它的作用前面已经讲过了，是控制高光产生的光斑的集中度。以一个球体为例，越接近光斑中心，半角向量和法线的夹角越小，高光越亮，越到光斑外围，半角向量和法线的夹角越大，高光越弱。听上去挺合理，但翻开物理课本回顾一下就会发现：理论上只有半角向量和法线完全重合的时候才有反射光线被视线接收到，凭什么这里还能允许它们存在夹角？而且夹角的变化还导致反射光线强度的变化，这个怎么来的？这里又有一个新的名词出现了：微表面。我们在渲染中是逐个像素进行处理的，每个像素虽然足够小了，但在这个像素覆盖的范围内还有无数细微的起起伏伏的物理结构，有起伏，就会有变化的法线。我们渲染时用到那个像素法线只能算是所有细微面的法线的平均值，实际上这个像素点内部朝各个方向的法线都是有的，只是所占比例有所不同。
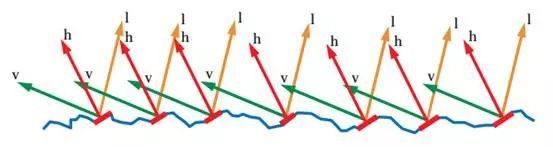
在渲染的时候我们当然不会把像素内部的法线逐个取出来再去计算光照，这么做也未免太二了，我们只需要把能反射到视线的法线所占的比例找出来，用它将高光强度修正一下就好了。其实我们常说的“半角向量”就是指能反射到视线的法线。
而我们讨论
的部分干的就是这个事，它根据半角向量和平均法线的夹角，计算出指向半角向量方向的微表面法线的比例。这么牛逼的事情一定要有个牛逼的名词来描述它，就叫“法线分布函数”，缩写为“NDF”，文中我们以D来表示。这样我们的BRDF就可以写成这样：
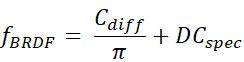
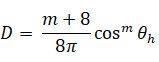
法线分布函数能解释表面上细微的凹凸不平对光的反射产生的影响，但是有一个前提：微表面上所有的点都能够接受到光线，并且能够反射出光线，事实上真实的物理表面大部分是达不到这样的条件的，如图所示：
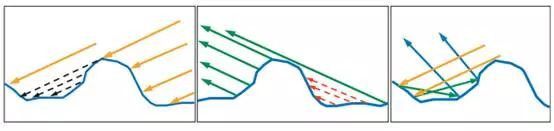
你看，在这样的凹凸的表面上，由于自身的遮挡，有很多点根本无法接受到入射光线，也有很多点反射的光线无法射出表面。因此，我们此处再定义一个函数叫“可见性函数”，本文中用V来表示。它的作用就是根据给定的入射光线和出射光线的方向，计算出不被自身遮挡的光线的比例。回头看看我们的BRDF公式里，貌似没有啊？没关系，请看：
定义V为常量1……怎么样？是不是被我的机智打败了。
最后只剩一个东西要讲解一下了，就是高光强度
，在公式中，这是个常量，但却不是符合真实物理规律的。在物理书讲反射与折射的章节上我们学过，在一个反射面上，当入射角度越“倾斜”，反射的光线越多，折射的光线越少，入射角度越“直”，折射的光线越多，反射的越少。这个现象叫做菲涅尔现象。所以这里的高光强度需要用一个函数来表示，本文写做F。在原公式中我们可以机智的认为它把这个函数也用一个常量函数来表示。
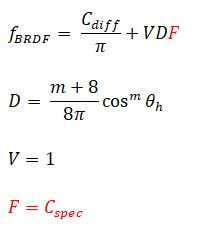
到此为止，我们已经成功把Blinn-Phong光照公式拆解成有物理意义的各个成分，从中也可以看到为什么我们说这个光照很“假”了：
1）法线分布函数的自变量基于一个没有太大物理意义的m。
2）菲涅尔函数是高光常量，表示完全没有考虑入射光线角度不同带来的反射变化。
3）可见性函数是常量1，表示所有微表面上的光线完全没有自遮挡。
4）漫反射和高光之间完全独立，没有考虑能量守恒的关系。
为了让光照达到真实的物理效果，我们就需要逐个解决上面的问题。
基于物理原理进行扩展
法线分布函数
首先看法线分布函数D，我们需要找一个更符合物理规律并且更容易控制的函数来代替原有的法线分布函数。在各种常见的PBR模型中被广泛使用的是Trowbridge-Reitz GGX函数：
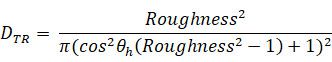
其中，Roughness就是我们常说的“粗糙度”，取值范围为0到1，当取值为1时表示最粗糙的表面，完全没有任何高光反射。这一点可以从公式中看出来。有的系统例如Unitiy里用“光滑度”来代替粗糙度，它们的关系是：粗糙度 = 1 - 光滑度。
菲涅尔系数
接下来看菲涅尔函数，我们知道当光垂直射向表面时，折射光线最多，反射光线最少，假设此时的菲涅尔系数是
，那么在给定任意角度的时候，可以用下面一个公式来近似的表示这个系数：
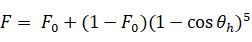
这个神秘的
是什么呢？它是在限定条件下折射和反射的比例，由物质的分子结构决定。是物质的天然属性。每一种物质都不相同。用一个更常见的说法，它叫做“反射率”。通常通一种物质对不同频谱的光反射率是不一样的，所以不管是F还是
都是一组RGB三通道的值。它的值到底是多少呢？先看一组通过真实物理实验得到的数据：
我们可以看到，非金属的反射率都非常小，而金属的反射率则比较高，大部分在0.5以上，RGB三个通道的差异体现了这种金属的颜色，值越大则金属越“亮”。
因此，对于非金属，我们其实可以用统一的一个比较小的值作为
，因为效果上差异不会太大，例如Unity引擎里将这个值定为常数（0.04, 0.04, 0.04），对于金属，我们以金属自身颜色Albedo作为它的值。理论上一种物质要么是金属，要么是非金属，不会出现介于金属和非金属之间的状态。但实际我们做3D渲染的时候，一个像素面积内是可能同时包含金属和非金属的。为了准确描述这种现象，我们定义一个值叫做“金属度”，当它为1时，反射率完全按金属的方式处理，为0时，完全按非金属的方式处理。当取值在0和1之间时，通过线性插值确定反射率：
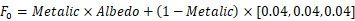
关于这个通过金属度计算出来的反射率，在下文中还有更多的意义，不过我们先接着看BRDF公式中剩下的最后一部分：可见性函数。
可见性函数
可见性函数是描述光线从入射到出射的过程中，有多少比例被微表面自身的凹凸不平遮挡住了。这个部分其实和法线分布有点像，依据的是表面的粗糙程度。为了准确描述，我们首先需要这样的一个函数：给一个方向，获得微表面在这个方向上被自遮挡的面积的比例。好的，大神们已经为我们准备好了这样的一个函数。
Schlick-GGX函数：
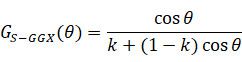
公式中的k其实是对粗糙度的一个简单变形，在只考虑一个固定方向的情况下，这个变形的公式为：
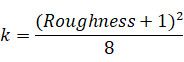
我们最终计算的可见性分了三部分：入射光线没被遮挡的部分、出射光线没被遮挡的部分、入射光线被遮挡后，在微表面内部多次反射又射出的部分。我们省略掉推导过程后，得到的公式是这样：
现在我们回顾一下BRDF公式：
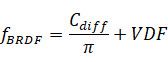
至此，公式中V、D、F三个部分我们都已经给出了结论，离最终的结果只剩下一步之遥了。
能量守恒
我们通常会把光照效果分为漫反射和镜面反射（既高光）两部分。 传统意义上说的“漫反射”是指凹凸不平的表面反射的没有方向性的光。但是我们已经在高光部分充分考虑了物体微表面的变化了啊。而且事实上我们把粗糙度调整为1时，效果跟我们预期的“漫反射”就是一样的。
而现在BRDF公式中的Diffuse实质上是这样的：光线射到表面上后，部分被反射，部分被折射而进入材质内部，在材质内部经过多次不规则的折射、反射后，部分光线被吸收，部分光线又从离射入点不远的地方射出来，这里的“不远”是指映射到屏幕后小于一个像素的大小。因此，材质反射率越高，则越多的光线被直接反射，越少的光线进入材质内部，Diffuse就越低。反之亦然。所以我们还需要两个系数来修正Specular和Diffuse两部分：
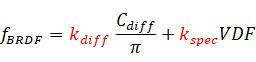
我们根据能量守恒的原则可知，Diffuse、高光能量之和一定小于或等于入射光的总能量，少的那部分是被吸收的部分，从前文的分析我们还可以肯定被吸收的部分一定是在被折射的光线中扣除的。从物理性质上来说，金属几乎吸收全量的折射光线，非金属则不怎么吸收光线。
根据这样过的几个性质，我们得到这样的近似的关系：首先高光系数其实就是前文所描的反射率
，因为它正好描述有多少光的能量会被高光反射出来。
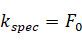
然后，Diffuse系数则是剩余部分扣除吸收的光线，而由于金属吸收光线，所以通过金属度来近似的计算吸收的光线比例：
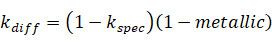
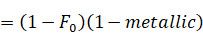
有了这个之后，PBR中能量守恒原则的得到描述，我们对前文提出的几个问题算是完成了回答。
总结
现在给出一个图来梳理一下本文中各个公式的关系：
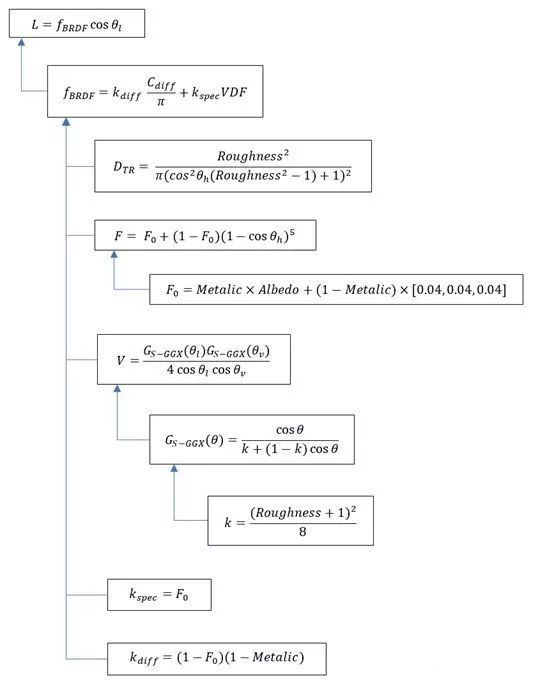
需要注意的是这里的各个部分的公式并不是唯一的公式。在各大游戏引擎中都有根据性能、效果、应用环境的不同而使用的不同算法。但思想是一致的。除此之外，还是建议大家继续研究正经一点的PBR理论基础，理解辐射度、光照能量等相关物理概念。以便在更复杂的光照环境中游刃有余的解决问题。
关于腾讯游戏学院专家团
如果你的游戏也富有想法充满创意，如果你的团队现在也遇到了一些开发瓶颈，那么欢迎你来联系我们。腾讯游戏学院聚集了腾讯及行业内策划、美术、程序等领域的游戏专家，我们将为全世界的创意游戏团队提供专业的技术指导和游戏调优建议，解决团队在开发过程中遇到的一系列问题。
项目指导合作请联系微信：18698874612
作者：董根
来源：腾讯GWB游戏无界
原地址：https://mp.weixin.qq.com/s/mgHA2uTFawAYjIcnSuW3Gw