之前在写笔记的时候就考虑到要写这一篇附录,因为笔者发现这一个主题涉及到的内容之多,足以单独拿出来讲一讲。加上赶上最近一个话题潮流——“如何看待游戏”。其实之前看了那么多探讨,很少有从技术方面来讨论关于这个话题的(不是指做游戏的技术)。先不论该怎么定义:“游戏的性质”这个问题——能不能作为“艺术载体”啊?导致成瘾是不是一个问题啊?这些探讨且都放到一边,单纯从技术发展的角度来说,游戏可能真的是不能缺少的一部分。以人工智能研发的角度来说,游戏是一个非常重要的范畴。
很多对于人工智能以及计算机科学的算法,都可以在游戏中获得实际应用。而反过来游戏也可以启发技术和算法的研发。《集异璧之大成》里面,人机博弈是一个相当重要的主题,尤其是关于人工智能的发展,以及我们研究人类思维的时候,这个内容是绕不过去的(很多游戏可以拿来作为研究大脑思维的实验)。
游戏某种程度上可以说是“把抽象思维表现到形式系统上面的一个过程”。游戏当中必须要制定规则,而在有限规则之下,以博弈的形式发展出多种多样,乃至于无穷无尽的变化,然后获得各种各样的结果。这里并不是在把游戏往高大上方面拉(而是确实就是如此),并且在严肃看待游戏的时候,确实可以从中受到很多启发。
回到GEB上面来说,之所以需要专门写这么一篇附录是因为:侯世达出版GEB的时候,当时的计算机技术和现在有着非常巨大的差距,如果直接看原书的内容,会让很多人觉得格格不入。尤其是书里面拿人机博弈来举例子,当时的例子放到今天来说已经没有说服力了——之前提到过GEB出版的时候,IBM的“深蓝”都还没有下赢国际象棋,更不说如今阿尔法狗都已经下赢围棋了。

二:游戏中的人机博弈
1·人工智能发展历史追溯
游戏与人工智能之间确实有着非常紧密的联系,这其中要牵扯到“博弈论”的内容。在人工智能的发展历史上的第二阶段,大概是二十世纪五十年代的时候,就涉及到了“博弈论”。
这里要稍微提一下人工智能的发展史,从概念上来说,人工智能的概念甚至可以追溯到早期神话传说时代就有雏形和概念了:神话、幻想当中的人造生命(炼金术里的人造小人)、自动机(上发条的非能源提供动力的可动机械——音乐盒、自动人偶、自动钢琴)、形式推理的发展和演进(之前曾经在读书笔记里提到关于形式推理的“推广部分”)、一直到现代计算机的发明。
几乎伴随着现代计算机的发明,计算机科学成立的同时,来自不同领域的数学家、心理学家、工程学家、经济学家、政治学家等一大批科学家都开始探讨关于创造人工大脑的可能性。1950年,图灵测试被提出来,图灵发表的划时代论文预言了创造出具有真正智能的机器的可能性。由于他注意到“智能”这一概念难以定义,所以他提出了著名的图灵测试。(GEB后半部分将会有大量篇幅提到这件事)。在1956年的时候,人工智能被正式确立为一门学科。
差不多就在同一时期,游戏AI就被引入了人工智能研究的课题里面。1951年,Christopher Strachey使用曼彻斯特大学的Ferranti Mark 1机器写出了一个西洋跳棋(checkers)程序;Dietrich Prinz则写出了一个国际象棋程序。亚瑟·山谬尔(Arthur Samuel)在五十年代中期和六十年代初开发的国际象棋程序的棋力已经可以挑战具有相当水平的业余爱好者。游戏AI一直被认为是评价AI进展的一种标准(这段内容在GEB里面,侯世达有详细的讲述)。
不止如此,早期的神经网络研究也差不多在这个时间开始了,早期的人工智能的研究是建立在20世纪30年代末到50年代初的一系列科学进展交汇的成果知识点,神经学研究发现大脑内由神经元组成的电子网络,激励电频只存在“开”、“关”两种状态,不存在中间态。同时期研究获得的控制论描述了电子网络的控制和稳定性,以及当时的信息论描述了数字信号的概念。图灵的计算理论证明了数字信号可以用来描述任何形式的计算。在这几者的结合之下,暗示了构建电子脑的可能性。但这个研究在70年代受到了挫折——实际上当时整个人工智能的研究都遭遇了瓶颈。
由于第一代人工智能的研究者太过于乐观,提出了太多过分乐观却没能实现的展望——比如1958年,艾伦·纽厄尔和赫伯特·西蒙说:“十年之内,数字计算机将成为国际象棋世界冠军。”“十年之内,数字计算机将发现并证明一个重要的数学定理。”(IBM的“深蓝”是97年的事)
1965年,赫伯特·西蒙说:“二十年内,机器将能完成人能做到的一切工作。”(这事到今天都没达到,除了科幻小说里)。
1967年,马文·闵斯基说:“一代之内……创造‘人工智能’的问题将获得实质上的解决。”(并没有)
1970年,马文·闵斯基:“在三到八年的时间里我们将得到一台具有人类平均智能的机器。”(笑而不语……)
在70年代初期的时候,人工智能的研究就进入了瓶颈期,当时最先进的AI程序都只能解决一些很简单的问题,而它们的问题在于一些基础性的障碍,而且这些问题至今都没有得到完美地解决。这些问题主要有这么几个:
1·计算机的运算能力,严格来说计算机要获得“智能”必须要在计算能力上突破一个界限,就好比飞机要达到一定速度才能飞起来。在这个界限之下,计算机的“智能”恐怕无法实现——目前来说这个界限依然模糊,虽然计算能力已经比当时强得多了。
2·计算复杂性和计算时间指数爆炸:这部分涉及到图灵、哥德尔等人研究的关于可计算性还有停机问题等等的研究,在GEB的内容里也有论述。比如一些证明等等,我们的大脑可以跨过步骤直达结果,而计算机要进行运算所需要的时间随着问题复杂性提升呈现指数爆炸。这部分也和计算机游戏部分相关,更复杂的问题需要更久的时间才能解决。这也是为什么,上个世纪末,国际象棋方面计算机获得了突破,而到现在围棋,才刚刚获得突破的原因(围棋的玩法远比国际象棋复杂得多,这点没人否认吧)。
在GEB这本书出版的时候,国际象棋已经有了几个具有一定水平的AI程序,然而其水平仅限于业余水平的高手,甚至还比不了职业高手,更不要说达到人类的峰值水平了(世界冠军)。而阿尔法狗和深蓝的事情得单独放到后面来说。

2·博弈论与游戏
那么说完那段时期的人工智能研究历史,我们来看看关于智能程序玩游戏和博弈论的内容:
“博弈论(英语:Game Theory),又译为对策论,或者赛局理论,经济学的一个分支,1944年冯·诺伊曼与奥斯卡·摩根斯特恩合著《博弈论与经济行为》,标志着现代系统博弈理论的的初步形成,因此他被称为“博弈论之父”。博弈论被认为是20世纪经济学最伟大的成果之一。目前在生物学、经济学、国际关系、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。主要研究公式化了的激励结构(游戏或者博弈)间的相互作用。是研究具有斗争或竞争性质现象的数学理论和方法。也是运筹学的一个重要学科。
博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。表面上不同的相互作用可能表现出相似的激励结构(incentive structure),所以它们是同一个游戏的特例。其中一个有名有趣的应用例子是囚徒困境。
具有竞争或对抗性质的行为称为博弈行为。在这类行为中,参加斗争或竞争的各方各自具有不同的目标或利益。为了达到各自的目标和利益,各方必须考虑对手的各种可能的行动方案,并力图选取对自己最为有利或最为合理的方案。比如日常生活中的下棋,打牌等。博弈论就是研究博弈行为中斗争各方是否存在着最合理的行为方案,以及如何找到这个合理的行为方案的数学理论和方法。
生物学家使用博弈理论来理解和预测进化(论)的某些结果。例如,John Maynard Smith和George R.Price在1973年发表于《自然》杂志上的论文中提出的“evolutionarily stable strategy”的这个概念就是使用了博弈理论。还可以参见进化博弈理论和行为生态学(behavioral ecology)。
博弈论也应用于数学的其他分支,如概率、统计和线性规划等。
——by:维基百科‘博弈论’词条。”(冯·诺依曼的名字在今天的电子计算机科学领域也可以说是如雷贯耳了)。
约翰·冯·诺伊曼
博弈论经过形式化和数学化之后获得了拓展,并且在应用上得到了推广。这里要是细究可以找出一大堆公式、函数还有理论分支出来。所以先到此为止。但是我们知道博弈论的内容涉及到了“游戏”背后的很多非常值得研究的内容,同时它也非常明显地展现出来了——“游戏的意义远远不只是玩,它也可以作为一种表现形式来展现一些更抽象和深奥的东西。”
如果以博弈论来看待在所有的“游戏”,我们发现不论何种形式,其根基都是一样的。数学家们通过数学归纳法,对游戏进行解构,从而寻找出必胜之道。可以说“游戏”是数学家们对于博弈论的研究以及对数学应用的一块重要领域(当然在现代游戏表面包装做得越来越花哨了,人们的注意力也就随之转移了)。但是一些非常古老的游戏依然具有着极其旺盛的生命力,并且一直延续到今天——比如:棋类游戏。棋类游戏的历史甚至可以追溯到人类历史的远古时期:中东跳棋、播棋、直棋、老虎棋等等。今天中国象棋、国际象棋、围棋、日本将棋流行于世界,甚至成为一种职业。(还有军仪,下军仪能拯救世界的……)这里要多提一句:西式战争类棋盘游戏,简称战棋,和我们泛指的棋类游戏有所不同,这里要稍微区别一下。
在棋类游戏里有多数都要依靠脑力取胜,所以称之为智力游戏不为过。自然也就成为了人工智能研究领域的课题之一。其中最早被拿来研究的是:井字棋游戏。
井字棋游戏相对于其他棋类游戏来说要简单一些,由于结构简单,成为人工智能研究领域里常被拿来当作博弈论和游戏搜索树(超前搜索树)的案例。据统计,井字棋游戏一共只有765个可能局面,26830个棋局。如果把对称的棋局视作不同局面,则可以有255168个棋局。正是由于这个结构简单,是最早被拿来进行编程的游戏,1952年为EDSAC电脑制作的井字棋游戏《OXO》是世界上最早的电脑游戏之一,电脑程序可以正确无误的和人类对手下棋。
但是随着进一步拓展,内容变得越来越复杂。人们把目光投向了国际象棋。

3·人机大战
编写可以和人类下国际象棋的电脑程序一直是人工智能领域里面的一个重要课题,很多科学家对此心向往之。在GEB当中侯世达也特别提到了这件事。当时的思路依然是依靠计算机的强大计算力,以超前搜索树为核心思路和人类对抗。但是这种暴力方式收效甚微,一直到GEB书出版的时候,国际象棋AI的水平只能和普通业余水平的高手较量,在职业领域里败多胜少。
棋盘是人机大战最早开始的战场,而实际上一直到今天还没有完全得出结论。因为虽然一直到1997年深蓝对决卡斯帕罗夫,计算机才第一次在棋盘上击败人类最高水平。但是现在来说这个差距并不大。尤其现在还有翻案,当年卡斯帕罗夫对绝“深蓝”的棋局似乎遭到了质疑。
其实整场对决持续了一年,卡斯帕罗夫和“深蓝”分别在1996年和1997年进行了对决。96年以卡斯帕罗夫4比2战胜了“深蓝”,之后IBM对“深蓝”进行了升级,计算能力达到了之前的两倍。在97年对决卡斯帕罗夫的时候以3.5比2.5战胜卡斯帕罗夫。但是这件事情现在来说有一些值得争议的地方。
超前搜索树
首先是97年那场棋局结束之后,卡斯帕罗夫再一次向“深蓝”提出挑战,但是IBM却拒绝了,并且迅速拆解了“深蓝”。在96年到97年这段时间,研究者对“深蓝”进行了针对卡斯帕罗夫下棋风格的针对性升级。同时卡斯帕罗夫指出,他在对局过程中明显感受到,电脑背后有人为操控的痕迹。(当时第二局的对局有很大的争议性)。因为在之后复盘的时候,人们发现“深蓝”犯下过一些打错,为卡斯帕罗夫把棋局打成和局留了空隙,而之后的对决里卡斯帕罗夫的状态显然也不是很好,犯了不少的错误——最后一局的时候“深蓝”之所以可以下赢,是因为卡斯帕罗夫颠倒了走棋次序。
而且在2003年的时候,卡斯帕罗夫分别还和两个更强的超级计算机对决过:X3D Fritz和Depp Junior(这台计算机的运算能力比97年版本的“深蓝”还要强一倍)。均能能获取胜局,并且两次对弈都以和局结束。也就是说即使在国际象棋中,计算机确实下赢了人类,但其优势也是非常微弱的。核心上依然是试图依靠暴力演算,靠计算力压倒人类对手。这算不上是“智能”的体现。
而在今天,谷歌研发的Alpha Go在围棋上战胜了人类顶尖高手。围棋的复杂程度远远超出象棋,因为其规则更简单,但是在棋盘上的局势非常抽象。围棋的程序研发并没有比象棋程序的起步晚太多,而一直到“阿尔法狗”之前,围棋程序的棋力和国际象棋之前一样,也都遇到了瓶颈。也就是说在此之前电脑打不过职业一定段位级别以上的人类高手。
在数学上,围棋具有着相当的启发性。过去沈括曾经猜测围棋的局面可能存在有10的127次方的数量。在复杂程度上,围棋的复杂程度几乎接近了计算复杂性理论当中“图灵机”利用多项式空间解决的判定问题集合:PSPACE的水平。(图灵机,也叫完备型图灵机,可以理解为抽象意义上的一种数学逻辑机。其可以复杂性可以等价于任何有限逻辑数学过程的终极强大的逻辑机器。围棋的复杂度已于1978年被Robertson与Munro证明为PSPACE-hard)。
围棋的着法,到了官子阶段(棋盘上被“活子”分割成了若干独立区域的时候),每个局部的对弈都有一个多项式级别的规范博弈树。(超前搜索树)这涉及到博弈论当中的组合博弈论,一般在象棋、围棋这种大型的博弈游戏里面,列出博弈树对于计算机的计算能力是一个难以应对的问题。(这也是为什么现在棋类程序能得到巨大的进步,就因为现在的计算机比起上个世纪的计算机,在计算能力方面已经获得了质的飞跃——当然“阿尔法狗”还是不一样的)所以通常计算机都会限制超前搜索树的层数,剔除不好的走法,一般而言搜索的层数越多,下出好棋的机会就多。

围棋
三:蒙特卡洛方法
“蒙特卡罗方法(英语:Monte Carlo method),也称统计模拟方法,是1940年代中期由于科学技术的发展和电子计算机的发明,而提出的一种以概率统计理论为指导的数值计算方法。是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。——by维基百科”
直白点来说:假设有一个有限的正方形空间,在这个空间上画出一个不规则图形。现在要求出这个不规则图形的面积。那这怎么做呢?用蒙特卡罗方法:向这个有限正方形空间内撒N(自然数,而且是很大的自然数)个微小颗粒(黄豆、BB弹啥的),而且这N个微小颗粒要撒的均用(都在平面上),平均的散布在这个正方形面积之内。然后我们来数一数撒在不规则图形内的有多少。假设有M个,则不规则图形的面积就等于M/N。N越大,计算出来的值就越精确。
这个方法是在20世纪40年代,在冯·诺伊曼,斯塔尼斯拉夫·乌拉姆和尼古拉斯·梅特罗波利斯在洛斯阿拉莫斯国家实验室为核武器计划工作时,发明了蒙特卡罗方法。因为乌拉姆的叔叔经常在摩纳哥的蒙特卡洛赌场输钱得名,而蒙特卡罗方法正是以概率为基础的方法。
“蒙特卡洛方法的伟大之处,在于对精确性问题无法解决的时候,利用“模拟”的思想来求解。在各个领域得以应用。本质是模拟(simulation):利用大量随机输入,产生各种输出;结果的概率分布就是真实分布的“近似”。所以,输入的分布是否随机(目前计算机所能做的就是伪随机,并不能产生真正的随机分布),这个过程我们称为Sampling Random Variables。
蒙特卡罗方法在金融工程学、宏观经济学、生物医学、计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算)机器学习等领域应用广泛。”
蒙塔卡洛计算方法与一般的数值计算方法有很大区别,它以概率统计理论作为基础进行计算。这个方法使得蒙特卡洛计算方法可以比较逼真地描述事务的特点还有物理实验的过程,从而解决一些数值方法难以解决的问题。
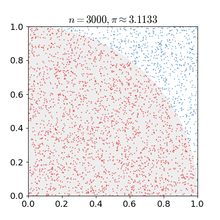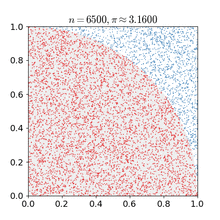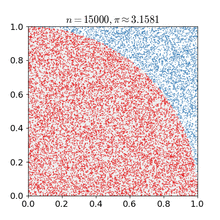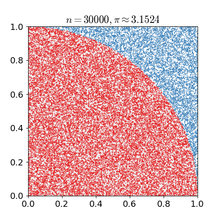
这个方法在电子游戏领域也得到了广泛的应用:
比如在射击游戏里面:假设一个射击者射击距离为R、在这个距离内射中数值为g(R)、射击者弹着点的分布密度还有一个函数——假设为f(R)。对于射击者的射击能力就能得出一个公式:<g>=0→∞g(R)f(R)dR
要注意<g>是一个随机变量(你不知道射击者射击水平怎么样),然后现在假设射击者设计了N次,则可以列出N次射击的弹着点数列:r1、r2、r3、r4……rn,把这个数列代入上面说的这个公式,就能获得射击能力数列:g(r1)、g(r2)……g(rn)。计算这个数列的算术平均值,也就是数列所有数之和除以N次,就获得了这个射击者的射击能力<g>的近似值(积分近似值)。则这个数就可以拿来在游戏中进行判断(游戏里还能设定设计次数什么的)。
通常蒙特卡洛方法通过构造符合一定规则的随机数来解决数学上的各种问题。对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题,蒙特卡洛方法是一种有效的求出数值解的方法。一般蒙特卡洛方法在数学中最常见的应用就是蒙特卡洛积分。
同样的带入到游戏当中,正因为蒙特卡洛方法能够比较逼真地描述具有随机性质的事物的特点以及物理实验过程,所以这个算法在电子游戏中,可以提高游戏的真实度,让玩家获得更多的乐趣。同时蒙特卡洛算法受几何条件的限制很小,而且还可以同时计算多个方案和多个未知量,所以即使是在复杂系统形状下依然可以使用,其泛用性比较广。(这样就不用担心算法和游戏系统本身起冲突了,而且能更高效的进行计算)。
当然在游戏的算法当中使用的不仅仅是蒙特卡洛算法,其它还有很多——不同算法对应不同问题,构建一个足够复杂的,更高可玩性的,更贴近现实的游戏数据系统。蒙特卡洛算法也常用于机器学习,特别是强化学习的算法中。一般情况下,针对得到的样本数据集创建相对模糊的模型,通过蒙特卡洛方法对于模型中的参数进行选取,使之于原始数据的误差尽可能的小。从而达到创建模型拟合样本的目的。
超复杂的搜索树
1·五大常用搜索算法
这里说到的五大常用算法分别是:贪心算法、回溯算法、分支限界算法、分治算法、动态规划
先来说说搜索算法基础概念:在计算机科学中,搜索算法是解决搜索问题的任何算法,即检索存储在某个数据结构中的信息,或者在问题域的搜索空间中计算的信息。这种结构的例子包括但不限于链表,数组数据结构或搜索树。合适的搜索算法通常取决于正在搜索的数据结构,并且还可能包括有关数据的先前知识。搜索还包含查询数据结构的算法,例如SQL SELECT命令。
搜索算法可以根据搜索机制进行分类。线性搜索算法以线性方式检查每个与目标关键字关联的记录。二进制或半间隔搜索,重复定位搜索结构的中心,并将搜索空间分成两半。比较搜索算法通过基于键的比较相继地消除记录来改进线性搜索,直到找到目标记录为止,并且可以按照定义的顺序应用于数据结构。数字搜索算法基于使用数字键的数据结构中的数字属性工作。最后,还需根据散列函数直接将键映射到记录。在线性搜索之外进行搜索需要以某种方式对数据进行排序。
算法的特征:(以下是高德纳在他的著作《计算机程序设计艺术》里对算法的特征归纳)
输入:一个算法必须有零个或以上输入量。
输出:一个算法应有一个或以上输出量,输出量是算法计算的结果。
明确性:算法的描述必须无歧义,以保证算法的实际执行结果是精确地匹配要求或期望,通常要求实际运行结果是确定的。
有限性:依据图灵的定义,一个算法是能够被任何图灵完备系统模拟的一串运算,而图灵机只有有限个状态、有限个输入符号和有限个转移函数(指令)。而一些定义更规定算法必须在有限个步骤内完成任务。
有效性:又称可行性。能够实现,算法中描述的操作都是可以通过已经实现的基本运算执行有限次来实现。
所以搜索算法对于游戏的进程有一定作用,通过这些搜索算法对于问题最优解的寻找,以及面对不同问题寻找不同的算法,可以构筑起游戏的多样性。
1)贪婪算法:贪婪算法可以得到问题的局部最优解,但是不一定能得到全局的最优解,同时获取最优解的好坏要看算法策略的选择。特点就是简单,能获取到局部最优解。同样的贪婪算法,不同的算法策略会导致得到差异非常大的结果。
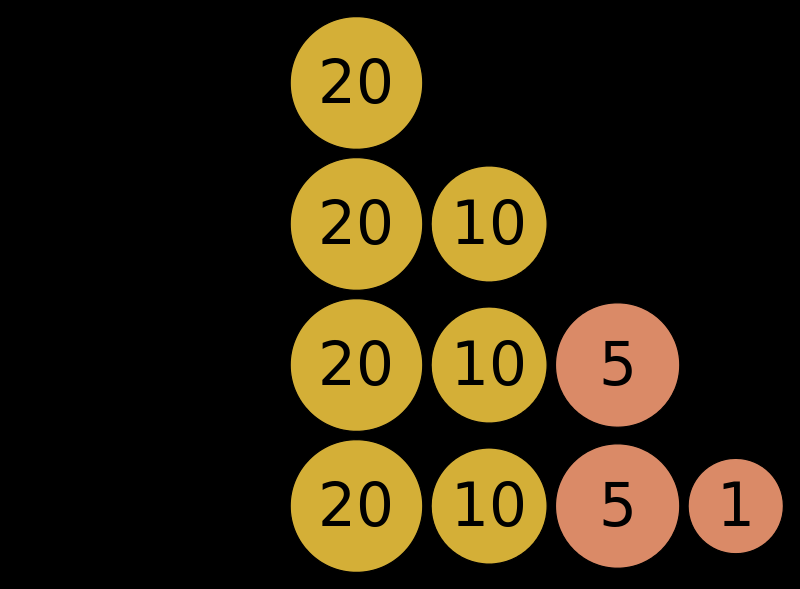
2)动态规划算法:当遇到最优化问题具有重复子问题和最优子结构的时候,就要利用动态规划了。动态规划算法的核心就是提供了一个记忆来缓存重复子问题的结果,避免了递归的过程中的大量的重复计算。动态规划算法的难点在于怎么将问题转化为能够利用动态规划算法来解决。当重复子问题的数目比较小时,动态规划的效果也会很差。如果问题存在大量的重复子问题的话,那么动态规划则能获得很高的效率。
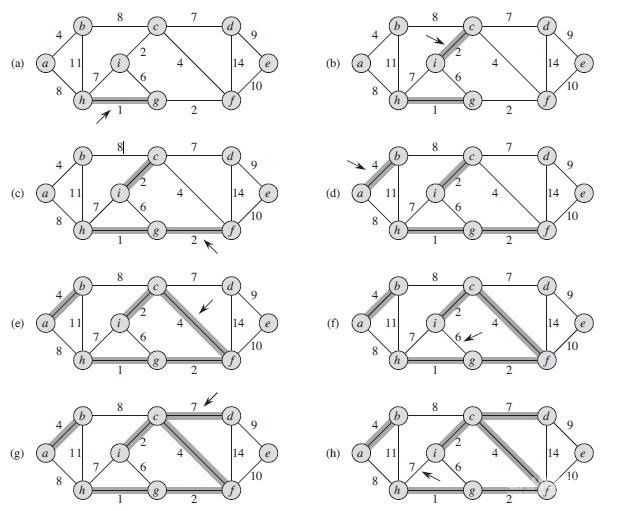
3)分治算法:分治算法就是把一个大的问题分为若干个子问题,然后在子问题继续向下分,一直到最基础简单问题,通过最简单问题的解决,通过小问题的解的总合成为大问题的解。分治算法是递归的典型应用。
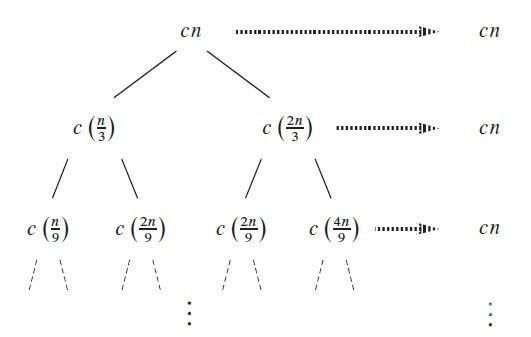
4)回溯算法:回溯算法是深度优先策略的典型应用,回溯算法就是沿着一条路向下走,如果此路不同了,则回溯到上一个分岔路,在选一条路走,一直这样递归下去,直到遍历万所有的路径。八皇后问题是回溯算法的一个经典问题,还有一个经典的应用场景就是迷宫问题。
回溯算法
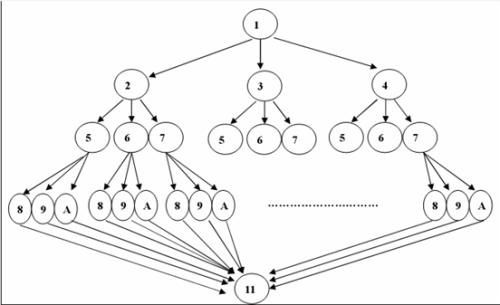
5)分支限界算法:回溯算法是深度优先,那么分支限界法就是广度或最小耗费优先的一个经典的例子。回溯法一般来说是遍历整个解空间,获取问题的所有解,而分支限界法则是获取一个最优解。
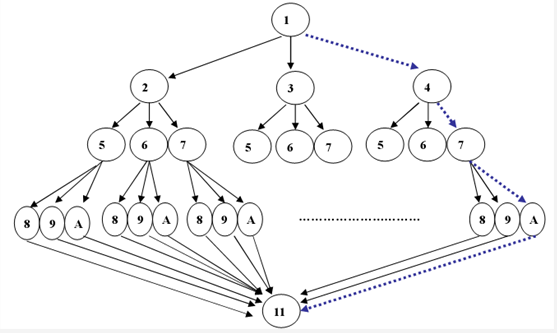
分支限界算法
那么这些算法在游戏中的应用如何呢?这里随便举几个例子。比如分治算法,可以应用到数组相关的快速排序当中去。——RPG游戏当中:按下数字按钮为游戏中获得的大量道具进行排序。(《仙剑奇侠传》)。
动态规划涉及到最大最小值的问题,在策略类游戏当中有非常鲜明的体现,比如warcraft、星际争霸当中,如何在有限资源下获得最高性价比兵种的部队组合呢?电脑AI有可能可以使用到这个算法,来进行特定资源数目下的兵种搭配,当然实际上来说要复杂些(因为数据一直在变)。
贪婪算法尽量实现以局部最优解产生全局最优解,这个在游戏中的运用非常多,最主要的一种就是游戏内目标路径的生成。当我们要求目标移动到制定目标点的时候,沿途的路径生成就可以依靠贪婪算法来生成(绕开障碍物,走最短距离)。
回溯算法最适合用来应对“迷宫”和搜索树的问题,尤其是搜索树,基本上棋类游戏都会遇上这个。回溯算法可以说是这两种问题的最优解搜索方法,每当遇到障碍的时候,回溯算法就会退回上一个节点进行重新选择,一直到走通为止。
分支限界算法在超前搜索树的运用上面,可以获得和回溯算法类似的效果,只不过两种算法的侧重点不同,前者以广度优先,后者以深度优先。这两者都被使用到棋类AI的程序当中去,并且获得了一定的成果。(对于棋局列出的超前搜索树,不同的搜索算法可以获得不同的走棋路数)。
2·蒙特卡洛搜索树
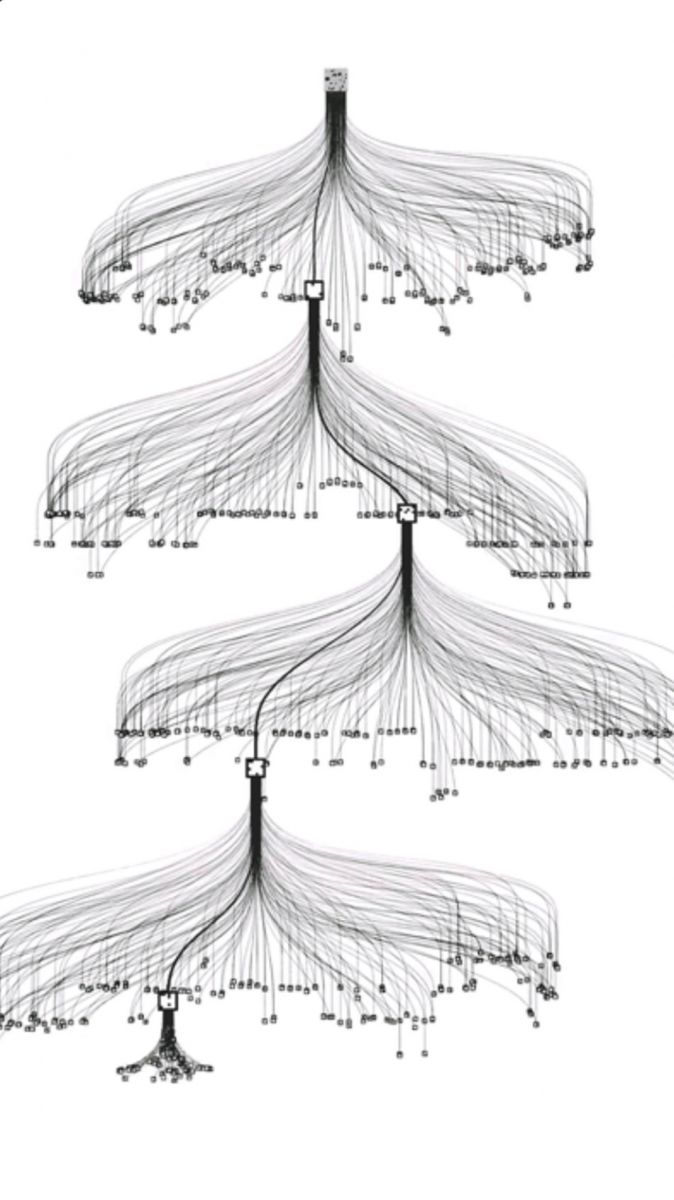
通过前面简短的介绍五大算法的运用,我们就知道搜索算法在游戏中地运用了。而游戏中,游戏树的结构基本上跑不掉,那么回溯前面的内容,蒙特卡洛算法也能够拿来与游戏搜索树进行结合。于是就有了蒙特卡洛搜索树:“蒙特卡洛树搜索(英语:Monte Carlo tree search;简称:MCTS)是一种用于某些决策过程的启发式搜索算法,最引人注目的是在游戏中的使用。一个主要例子是计算机围棋程序,它也用于其他棋盘游戏、即时电子游戏以及不确定性游戏。”
以搜索树来看待这个方法的应用,搜索树也可以以纵横轴来看——广度和深度。那么我们假设:每个节点都有b个选择以及到达目标的深度d,一个毫无技巧的算法通常都要搜索“b的d次”方个节点才能找到答案。所以随着游戏复杂度的提升,对计算机的计算能力要求呈现指数增长。像是围棋这样的游戏在早先,对于计算机来说,这个搜索树就算不动了。所以行之有效的办法是剔除掉多余的分支,把搜索计算集中到良性的选择分支上面(能赢),所以这里就需要用到启发式算法。启发式算法借由使用某种切割机制降低了分叉率以改进搜索效率,启发式计算为每个要解决特定问题的搜索树的每个节点提供了较低的分叉率,因此它们拥有较佳效率的计算能力。选择子结点的主要困难是在较高平均胜率的移动后对深层次变型的利用和对少数模拟移动的探索二者中保持某种平衡。
最能感受到启发式算法好处的经典问题是数字推盘游戏(n-puzzle)。此问题在计算错误的拼图图形,与计算任两块拼图的曼哈顿距离的总和以及它距离目的有多远时,使用了蒙特卡洛算法。注意,上述两条件都必须在有限的范围内。
早在20世纪40年代的时候布鲁斯·艾布拉姆森(Bruce Abramson)在他1987年的博士论文中就探索了这一想法,称它:“展示出了准确、精密、易估、有效可计算以及域独立的特性“。他用蒙特卡洛方法深入试验了井字棋,然后进一步的试验了黑白棋和国际象棋的机器生成的评估函数。
1992年,B·布鲁格曼(B.Brügmann)首次将蒙特卡洛方法应用于对弈程序,但他的想法在当时并未获得重视。2006年堪称围棋领域蒙特卡洛革命的一年,雷米·库洛姆(Remi Coulom)描述了蒙特卡洛方法在游戏树搜索的应用并命名为蒙特卡洛树搜索。之后列文特·科奇什(Levente Kocsis)和乔鲍·塞派什瓦里(Csaba Szepesvári)开发了UCT算法(上限置信区间算法,是一种博弈树搜索算法,该算法将蒙特卡洛树搜索方法与UCB公式结合,在超大规模博弈树的搜索过程中相对于传统的搜索算法有着时间和空间方面的优势。)
西尔万·热利(Sylvain Gelly)等人在他们的程序MoGo中实现了UCT。2008年,MoGo在九路围棋中达到段位水平,Fuego程序开始在九路围棋中战胜实力强劲的业余棋手。2012年1月,Zen程序在19路围棋上以3:1击败二段棋手约翰·特朗普(John Tromp)。自2006年以来,最优秀的程序全部使用蒙特卡洛树搜索。
除此之外蒙特卡洛树搜索也被用于其他棋盘游戏程序,比如六贯棋、三宝棋、亚马逊棋和印度斗兽棋;在即时电子游戏里:如《吃豆小姐》、《神鬼寓言:传奇》、《罗马II:全面战争》;桌面游戏,如斯卡特、扑克、万智牌、卡坦岛。
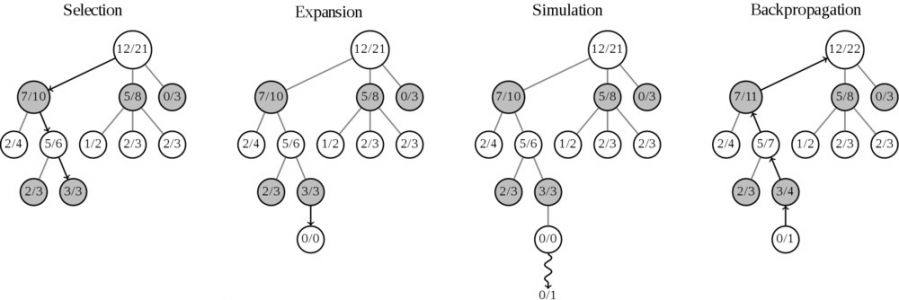
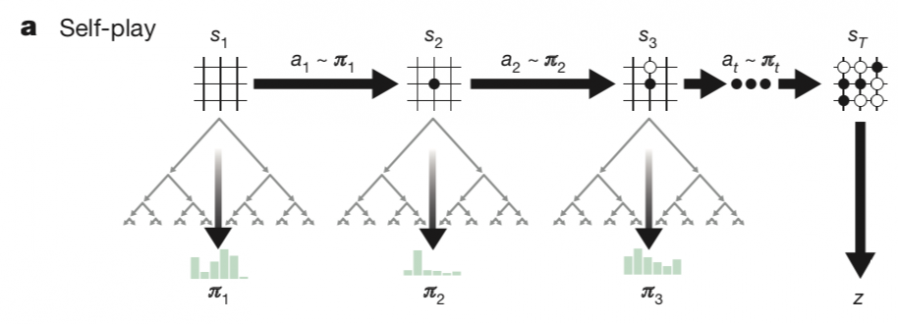
蒙特卡洛树搜索有四个步骤:
1·选择(Selection):从第一个节点开始,选择连续的子节点向下至分支节点X。后面给出了一种选择子节点的方法,让游戏树向最优的方向扩展,这是蒙特卡洛树搜索的精要所在。
2·扩展(Expansion):除非任意一方的输赢使得游戏在子节点X结束,否则创建一个或多个子节点并选取其中一个节点Y。
3·仿真(Simulation):在从节点Y开始,用随机策略进行游戏。
4·反向传播(Backpropagation):使用随机游戏的结果,更新从节点Y到节点X的路径上的所有节点信息,每一个节点的内容代表胜利次数/游戏次数。
四:人工神经网络——深度学习
现在在人工智能的范畴内,神经网络是一个热门话题。它在公众当中的话题度多少是来自于AlphaGo“阿尔法狗”下赢围棋这件事,那我们不妨来看一看现在说的人工神经网络和深度学习这回事。实际上这两个概念不能直接混为一谈,要想说清楚还得来看看人工智能的发展史,并且给几个子范畴进行一下划分,因为我们知道人工智能是一个综合的、多个研究领域的总称。
人工智能的研究历史有着一条从以“推理”为重点,到以“知识”为重点,再到以“学习”为重点的自然、清晰的脉络。而机器学习是人工智能的一个分支,以机器学习为手段解决人工智能中的问题,是实现人工智能的一个途径。
机器学习理论主要是设计和分析一些让计算机可以自动“学习”的算法。机器学习算法是一类从数据中自动分析获得规律,并利用规律对未知数据进行预测的算法。因为学习算法中涉及了大量的统计学理论,机器学习与推断统计学联系尤为密切,也被称为统计学习理论。算法设计方面,机器学习理论关注可以实现的,行之有效的学习算法。很多推论问题属于无程序可循难度,所以部分的机器学习研究是开发容易处理的近似算法。目前机器学习已广泛应用于数据挖掘、计算机视觉、自然语言处理、生物特征识别、搜索引擎、医学诊断、检测信用卡欺诈、证券市场分析、DNA序列测序、语音和手写识别、战略游戏和机器人等领域。
之所以要先说机器学习,是因为深度学习属于机器学习的一个分支领域。它的基础是机器学习中的分散表示(distributed representation)。分散表示假定观测值是由不同因子相互作用生成。在此基础上,深度学习进一步假定这些相互作用的过程可分为多个层次,代表对观测值的多层抽象。不同的层数和层的规模可用于不同程度的抽象。(分层概念在笔记的整篇里有过大量的描述,差不多是那样的概念:机器语言层到运行界面层)
深度学习运用了这分层次抽象的思想,更高层次的概念从低层次的概念学习得到。这一分层结构常常使用贪心算法逐层构建而成,并从中选取有助于机器学习的更有效的特征。不少深度学习算法都以无监督学习的形式出现(以“阿尔法狗”举例子来说,它除了和人类选手实战之外,也可以自我对弈,没有给定事先标记过的训练示例,自动对输入的数据进行分类或分群),因而这些算法能被应用于其他算法无法企及的无标签数据,这一类数据比有标签数据更丰富,也更容易获得。这一点也为深度学习赢得了重要的优势。
而一部分最成功的深度学习方法涉及到对人工神经网络的运用,在上面关于人工智能的研发历史当中我们就已经知道了,人工神经网络的研究时间基本等同于人工智能本身。虽然在中间一段时间经历了一些外在原因,以及自身技术的限制,停滞了一段时间。人工神经网络在机器学习和认知科学领域,作为一种模仿生物神经网络(中枢神经系统,特别是大脑)的结构和功能的数学模型或计算模型,用于对函数进行估计或近似。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构,是一种自适应系统,通俗的讲就是具备学习功能。
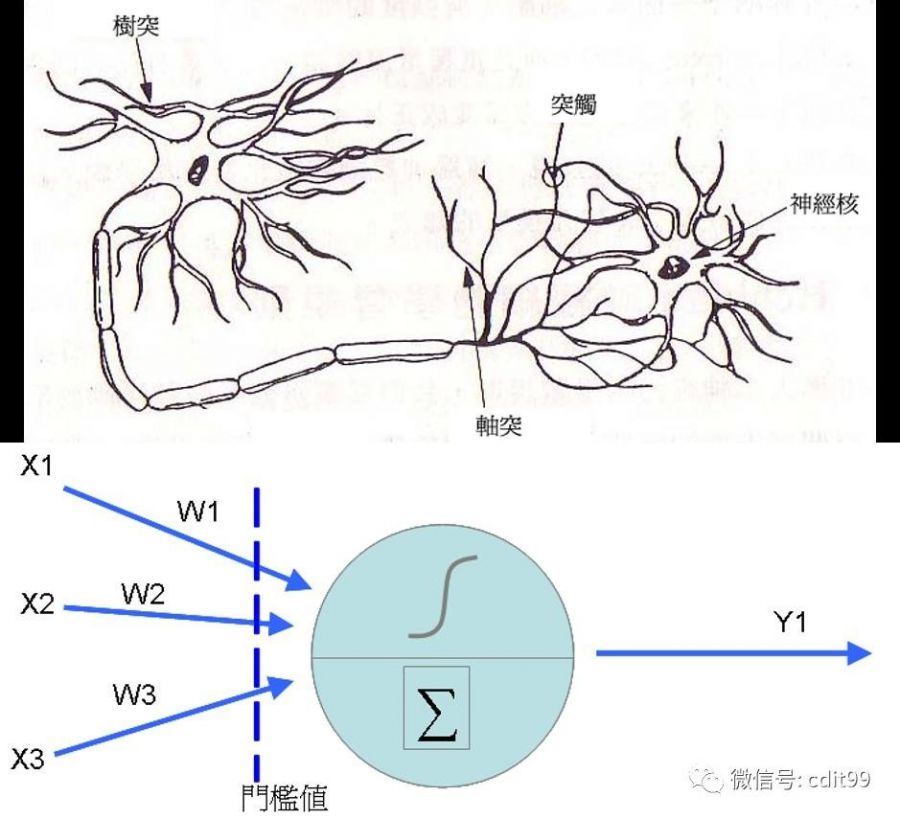
之前在笔记整篇内容里大概介绍过人工神经网络的启发原理:神经元之间的联结关系。不同的模式会激发神经元之间的不同联系——比如一个固定模式下,神经元A和B的电突触之间必须经常激活信号连接的话,二者的电突触连接就会变得比一般神经元之间的信号连接更强(更活跃,效能更强)。——神经科学中的赫布理论。但这个原理只是奠基,到我们今天看到的这个人工神经网络还有一定的距离。
依据赫布理论开发的人工神经网络出现了两个关键问题:第一是基本感知机无法处理异或回路。第二个重要的问题是计算机没有足够的能力来处理大型神经网络所需要的很长的计算时间。直到计算机具有更强的计算能力之前,神经网络的研究进展缓慢。后来出现的一个关键的进展是反向传播算法。这个算法有效地解决了异或的问题,还有更普遍的训练多层神经网络的问题。
在20世纪80年代中期,分布式并行处理(当时叫作联结主义)流行起来。神经网络传统上被认为是大脑中的神经活动的简化模型,虽然这个模型和大脑的生理结构之间的关联存在争议。人们不清楚人工神经网络能多大程度地反映大脑的功能。所以之后支持向量机和其他更简单的方法(例如线性分类器)在机器学习领域的流行度逐渐超过了神经网络,但是在2000年代后期出现的深度学习重新激发了人们对神经网络的兴趣。
在人工神经网络的现代软件实现中,被生物学启发的那种方法已经很大程度上被抛弃了,取而代之的是基于统计学和信号处理的更加实用的方法。在一些软件系统中,神经网络或者神经网络的一部分(例如人工神经元)是大型系统中的一个部分。这些系统结合了适应性的和非适应性的元素。虽然这种系统使用的这种更加普遍的方法更适宜解决现实中的问题,但是这和传统的联结主义人工智能已经没有什么关联了。不过它们还有一些共同点:非线性、分布式、并行化,局部性计算以及适应性。从历史的角度讲,神经网络模型的应用标志着二十世纪八十年代后期从高度符号化的人工智能(以用条件规则表达知识的专家系统为代表)向低符号化的机器学习(以用动力系统的参数表达知识为代表)的转变。
“2006年之后人们用CMOS创造了用于生物物理模拟和神经形态计算的计算设备。最新的研究显示了用于大型主成分分析和卷积神经网络的纳米设备具有良好的前景。如果成功的话,这会创造出一种新的神经计算设备,因为它依赖于学习而不是编程,并且它从根本上就是模拟的而不是数字化的,虽然它的第一个实例可能是数字化的CMOS设备。
在2009到2012年之间,Jürgen Schmidhuber在Swiss AI Lab IDSIA的研究小组研发的递归神经网络和深前馈神经网络赢得了8项关于模式识别和机器学习的国际比赛。例如,Alex Graves et al.的双向、多维的LSTM赢得了2009年ICDAR的3项关于连笔字识别的比赛,而且之前并不知道关于将要学习的3种语言的信息。
IDSIA的Dan Ciresan和同事根据这个方法编写的基于GPU的实现赢得了多项模式识别的比赛,包括IJCNN 2011交通标志识别比赛等等。他们的神经网络也是第一个在重要的基准测试中(例如IJCNN 2012交通标志识别和NYU的扬·勒丘恩(Yann LeCun)的MNIST手写数字问题)能达到或超过人类水平的人工模式识别器。
类似1980年Kunihiko Fukushima发明的neocognitron和视觉标准结构(由David H.Hubel和Torsten Wiesel在初级视皮层中发现的那些简单而又复杂的细胞启发)那样有深度的、高度非线性的神经结构可以被多伦多大学杰夫·辛顿实验室的非监督式学习方法所训练。——by维基百科”
目前人工神经网络没有一个统一的正式定义。不过,具有下列特点的统计模型都可以被称作是“神经化”的:
1·具有一组可以被调节的权重(被学习算法调节的数值参数,模仿神经元之间的激发)。
2·可以估计输入数据的非线性函数关系。
3·这些可调节的权重可以被看做神经元之间的连接强度。

五:解析“阿尔法狗”
我们来看看目前人机博弈的最前沿,代表计算机一方的最高水平的代表——AlphaGo“阿尔法狗”。根据官方公布的资料,“阿尔法狗”的原理非常明确:在蒙特卡洛树搜索算法的核心基础上搭载两个深度学习的人工神经网络;其中一个负责预判布局,另一个负责落子。蒙特卡洛树搜索在围棋当中的应用已经很早就有了,而且也是取得最好成绩的算法。(这在上面已经说过了)。
而深度学习原本主要应用是图像分析,利用计算机模拟神经元,可以训练计算机有类似人类“直觉”的反应,2014年左右,Google、DeepMind和facebook等公司意识这可能可以用在处理计算机围棋。最直接的想法是输入人类的围棋棋谱,并在程序中设置围棋规则,以及各棋谱的最后胜负局面,利用监督学习让计算机得到“棋感”——对局面进行判断,计算机因而可以给出特定局面下有哪些可能的行棋方法,后来这个方法在AlphaGo的论文中被称为“走子网”。深度学习是最先在某些识别任务上达到和人类表现具备同等竞争力的算法。在此基础之上以蒙特卡洛树搜索为核心,以极高的效率进行运算(蒙特卡洛算法对于复杂超前搜索树的预算效率很高),同时以神经网络对每一步的局面进行判断。
“历史:
一般认为,计算机要在围棋中取胜比在国际象棋等游戏中取胜要困难得多,因为围棋的下棋点极多,分支因子大大多于其他游戏,而且每次落子对情势的好坏飘忽不定,诸如暴力搜索法、Alpha-beta剪枝、启发式搜索的传统人工智能方法在围棋中很难奏效。在1997年IBM的计算机“深蓝”击败俄籍世界国际象棋冠军加里·卡斯帕罗夫之后,经过18年的发展,棋力最高的人工智能围棋程序才大约达到业余5段围棋棋手的水准,且在不让子的情况下,仍无法击败职业棋手。2012年,在4台PC上运行的Zen程序在让5子和让4子的情况下两次击败日籍九段棋手武宫正树。2013年,Crazy Stone在让4子的情况下击败日籍九段棋手石田芳夫,这样偶尔出现的战果就已经是难得的结果了。
AlphaGo的研究计划于2014年引导,此后和之前的围棋程序相比表现出显著提升。在和Crazy Stone和Zen等其他围棋程序的500局比赛中,单机版AlphaGo(运行于一台计算机上)仅输一局。而在其后的对局中,分布式版AlphaGo(以分布式运算运行于多台计算机上)在500局比赛中全部获胜,且对抗运行在单机上的AlphaGo约有77%的胜率。2015年10月的分布式运算版本AlphaGo使用了1,202块CPU及176块GPU。
2015年10月,AlphaGo击败樊麾,成为第一个无需让子即可在19路棋盘上击败围棋职业棋手的计算机围棋程序,写下了历史,并于2016年1月发表在知名期刊《自然》。
2016年3月,透过自我对弈数以万计盘进行练习强化,AlphaGo在一场五番棋比赛中4:1击败顶尖职业棋手李世石,成为第一个不借助让子而击败围棋职业九段棋手的计算机围棋程序,立下了里程碑。五局赛后韩国棋院授予AlphaGo有史以来第一位名誉职业九段。
2016年7月18日,因柯洁那段时间状态不佳,其在Go Ratings网站上的WHR等级分下滑,AlphaGo得以在Go Ratings网站的排名中位列世界第一,但几天之后,柯洁便又反超了AlphaGo。2017年2月初,Go Ratings网站删除了AlphaGo、DeepZenGo等围棋人工智能在该网站上的所有信息。
2016年12月29日至2017年1月4日,再度强化的AlphaGo以“Master”为账号名称,在未公开其真实身份的情况下,借非正式的网络快棋对战进行测试,挑战中韩日台的一流高手,测试结束时60战全胜。
2017年5月23至27日在乌镇围棋峰会上,最新的强化版AlphaGo和世界第一棋手柯洁比试、并配合八段棋手协同作战与对决五位顶尖九段棋手等五场比赛,获取三比零全胜的战绩,团队战与组队战也全胜,此次AlphaGo利用谷歌TPU运行,加上快速进化的机器学习法,运算资源消耗仅李世石版本的十分之一。在与柯洁的比赛结束后,中国围棋协会授予AlphaGo职业围棋九段的称号。
AlphaGo在没有人类对手后,AlphaGo之父杰米斯·哈萨比斯宣布AlphaGo退役。而从业余棋手的水平到世界第一,AlphaGo的棋力获取这样的进步,仅仅花了两年左右。最终版本Alpha Zero可自我学习21天达到胜过中国顶尖棋手柯洁的Alpha Go Master的水平。——维基百科‘阿尔法狗’词条。”
六:后记
侯世达在阿尔法狗的围棋战胜李世石之后有发表过说话,他说,现在的“智能程序”确实能做到一些很厉害的事,但是距离所谓的“智能”还差距很大——具体怎么说的笔者不确定,大概是这么个意思。在这一点上笔者非常赞同。
联想到之前甚嚣尘上的关于人工智能的各种展望和公众话题,现在这么看来确实有些——矛盾吧(当然看问题的角度都不一样,得到的结论自然不一样)。核心问题可能在于我们对于人工智能的期盼究竟是什么?关于这个笔者觉得机核小李老师的几期电台说的挺好,而且笔者自己在写这篇投稿的时候,也一直在放电台(再三感谢小李老师)。这篇附录是读书笔记系列的第一篇,之后还有没有不敢确定,说不定可能还有。
非常感谢一直看下来的读者朋友,谢谢!
作者:丑客
来源:机核
原地址:https://www.gcores.com/articles/110664